抖音t0t1t2t3是什么意思
根据单向体内原则,各组成环(轴d1除外)的极限偏差可定为:
d2=d5=5(0~-0.018)
d=30(0~-0.033)
d4=2(0~-0.02)所以,各环中间偏差Δ i =( ESi + EI i )/2
ESi —第i个组成环的极限上偏差;Ei —第i个组成环的极限下偏差;
0 =0.075
Δ 2 =Δ 5 =-0.024
Δ 3 =-0.042
Δ 4 =-0.01
∴Δ 1=0.075+(-0.024-0.042-0.01-0.024)=-0.025

公差校验方法
现有一滑块在滑槽内滑动,要求滑块上半部分与滑槽上半部分间隙 0.3mm
≤Δ =x+y≤0.8mm。 已知各尺寸: A1= 34(0~+0.1) , A2= 40(0~+0.1 ), A3= 33(0~-0.14),A4=40(-0.04~-0.08)如下图 1、图 2 所示。
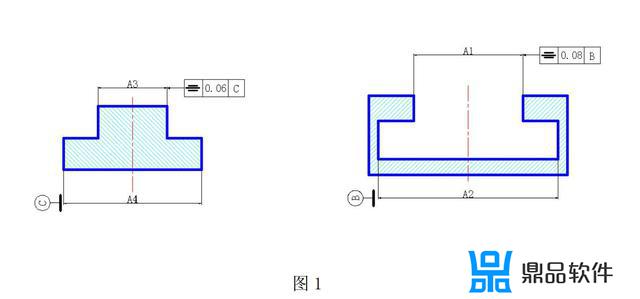
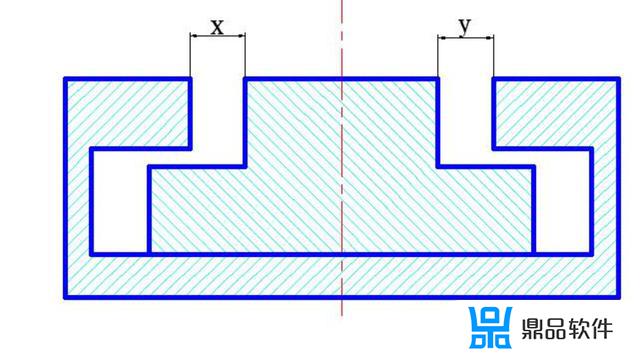
图2
由上面 2 图可以看出:对称度误差会影响到上部侧面间的间隙 x、y 的大小。
对称度公差与尺寸公差大小的比值最大为 3.5,所以,我们不能忽略形位公差的
影响。换句话说,被测中心面对基准中心面的偏移也构成尺寸链中的一环。为了
计算方便,我们可以使用极限状况工作下零件的位置,假定两工件的下半部一侧
紧靠在一起进行计算。如图 3:
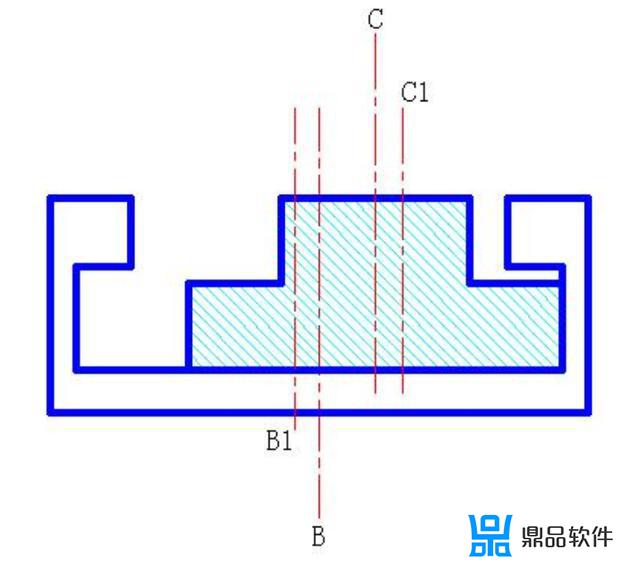
图3
由于上部的间隙分布于中心面的两侧,所以,我们需要建立两个尺寸链分别
计算其间隙大小,然后求两个间隙的极限范围并集。如图 4(右侧间隙尺寸链)、
图 5(左侧间隙尺寸链)所示:
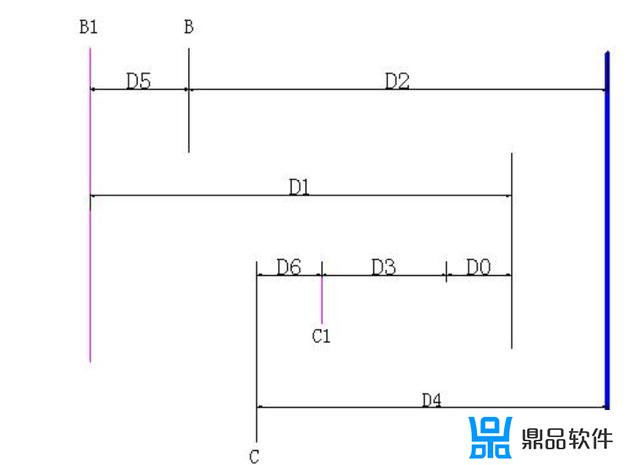
图4
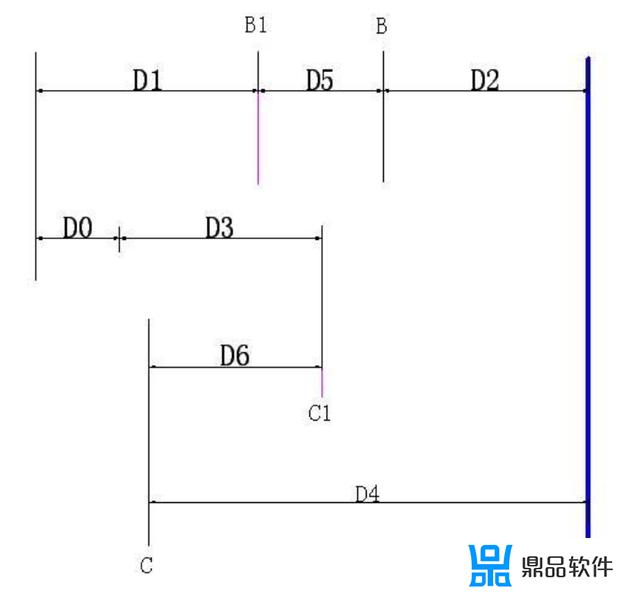
图5
首先,解释一下图 4、图 5 中代号和几条线的意义:
蓝色粗实线为紧靠之一边;
细实线 B 为滑槽上部基准中心平面,细实线 B1 为滑槽上部实际中心面,对
应图 3 中相应中心线;
细实线 C 为滑块上部基准中心平面,细实线 C1 为滑块上部实际中心面,对
应图 3 中相应中心线;

现在,进入计算环节。
上部右侧间隙:
T1 = ES1 - EI1 =0.07- 0 =0.07
T2 = ES2 - EI2-0.05-0=0.05
T2=0.05 T3=0.07 T4=0.02 T5=0.08 T6=0.06
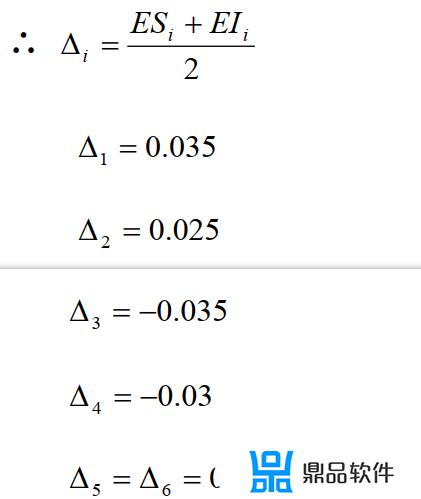
显然,由图 4 中可以看出:D1、D4 是增环,D2、D3、D5、D6 是减环。
∴ 封闭环 D0=(D1+D2)-(D3+D4)=(17+20)-(16.5+20)=0.5
Δ 0 = (Δ1 + Δ 4 ) - (Δ 2 + Δ3 + Δ5 + Δ 6 ) = 0.015
T0 = T1 + T2 + T3 + T4 + T5 + T6 = 0.35
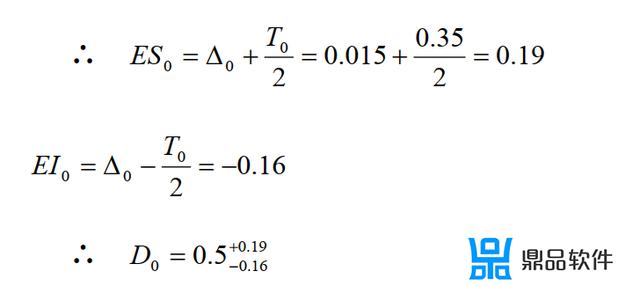

如果上述结果不符合题设条件,则需要重新设计分配公差。
本节类容详细介绍了直线尺寸链的解算和验证方法方法, 请诸位仔细阅读以
便于在将来的实际工作中可以根据具体情况解算尺寸链,合理的赋予各尺寸
公差,而不是盲目地提高零件公差等级而导致加工难度加大,成本提高。当
然了,我们并不是要求所有的公差都通过尺寸链解算得出来,这对于机械设
计来说也是不现实的;但是,建议对于所设计的设备非常重要的零部件而且
精度要求又很严格的地方的公差通过解算得出来,以防止给出的精度富裕,
提高加工成本和难度。
以上就是抖音t0t1t2t3是什么意思的详细内容,更多内容请关注鼎品软件其它相关文章!